Observing Time Estimate for APEX-2A
On this page we will show how to estimate the observing times with the APEX 345 GHz receiver.
The equivalent system temperature outside the atmosphere is calculated from the expression:
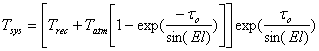 |
(1) |
where Trec is the receiver temperature, Tatm is the integrated physical atmospheric temperature (normally about 270 K), τo is the atmospheric zenith opacity and El the elevation of the source. Table 1 lists typical values of the atmospheric zenith opacity at Chajnantor. Eq. (1) provides only a rough estimate (the atmospheric transmission page provides more accurate values), but good enough for most applications. The fact that the telescope also picks up some signal from the ground is not taken into account.
ν [GHz] |
290 |
345 |
358 |
372 |
τo |
0.05 |
0.09 |
0.12 |
0.5 |
Table 1: Typical zenith opacities at Chajnantor during good conditions (pwv = 0.5 mm)
The rms noise in the spectrum is calculated from:
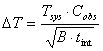 |
(2) |
where Cobs is a factor depending on the observing method used, B
is the noise bandwidth per channel of the spectrometer and tint the
integration time ON source. C is equal to
![]() for
switching and position switching (because noise is added when the OFF spectrum
is subtracted from the ON spectrum) and 1 for frequency switching. Solving for
tint in Eq. (2), we get
for
switching and position switching (because noise is added when the OFF spectrum
is subtracted from the ON spectrum) and 1 for frequency switching. Solving for
tint in Eq. (2), we get
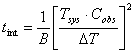 |
(3) |
As an example we will now calculate the integration time necessary in order
to obtain an r.m.s. noise of 0.1 K with the FFTS bandwidth of 1 GHz at 345 GHz
using the various observing methods. The elevation of the source will be assumed
to be 60° and the zenith opacity at 345 GHz is about 0.09 (Table 1). The
receiver temperature as a function of frequency is shown in Fig. 1 and is about
70 K at 345 GHz. This gives Tsys = 106 K which corresponds to a SSB
value of 212 K. For beam and position switching
Cobs = ![]() and we want to obtain a ΔT of 0.1 K which gives tint = 1.2 min.
For beam and position switching this value has to be multiplied by a factor depending
on the time spent in the OFF position and an overhead time which includes telescope
movements and calibrations. We will assume a value of 3.2 for this factor. The total
time for the observation is thus 3.8 min.
and we want to obtain a ΔT of 0.1 K which gives tint = 1.2 min.
For beam and position switching this value has to be multiplied by a factor depending
on the time spent in the OFF position and an overhead time which includes telescope
movements and calibrations. We will assume a value of 3.2 for this factor. The total
time for the observation is thus 3.8 min.
The estimated rms noise values should of course be compared with the expected signal intensity. The main beam and moon efficiencies of APEX at 345 GHz are expected to be 0.85 and 1.0, respectively. Thus, a CO(3-2) line with a brightness temperature of 10 K would give an intensity of 10 * 0.85 = 8.5 K, if the source just fills the main beam, or 10 * 0.9=9 K, if the source is extended.




